Introduction by Cathy Williams
Maybe some of you recall from childhood, discovering a set of 6 little cardboard cards filled with numbers that came as a prize in a Cracker Jack Box? I clearly remember the day I got this prize. I was fascinated that it always worked, playing it over and over again with anyone who would engage me. I carried the cards with me everywhere and eventually they ended up wet mush after spinning through the washing machine in the pocket of my pants. Decades later they were reintroduced into my life. It was Christmas day in London and everyone was excited about “crackers.” I didn’t understand the excitement until Jo explained that it was a little game between two people where the winner got a prize – not food. Guess what prize I won? The 6 cards were back in my life!
Here they are presented to you as a low floor/high ceiling task. The name of this task has to be Crackers, since it started with Cracker Jacks and came back to me from pulling and winning a Cracker.
Directions
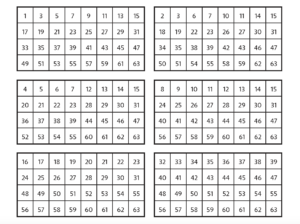
- Ask a partner to pick a number between 1 and 63 and not tell you.
- Show one of the 6 cards and ask, “Is your number on this card?”
- If they say yes record the first number in the upper left hand corner of the card. If they answer “no”, record nothing.
- Show the second card. Ask, “Is your number on this card?”
- If they say yes record the first number in the upper left hand box of the card. If no, record nothing.
- Continue until you have shown all 6 cards.
- The number your partner chose is the sum of the numbers you recorded.
- The goal is for students to record and find the sum of the numbers without pencil and paper, however not being there yet should not keep them from playing or make them feel lesser. They just aren’t there yet!
Task
- What do you notice & wonder?
- Create a convincing argument showing why this works. Can you make a visual proof?
- Make a presentation showing how this puzzle might have been created.
- If you were going to continue this pattern, what would the 7th card look like? What would be the greatest number your partner could choose if you had 7 cards? Would the puzzle still work?