Fluency Without Fear: Research Evidence on the Best Ways to Learn Math Facts
By Jo Boaler, Professor of Mathematics Education, co-founder youcubed
With the help of Cathy Williams, co-founder youcubed & Amanda Confer, Stanford University
Updated January 28th, 2015
Introduction
A few years ago a British politician, Stephen Byers, made a harmless error in an interview. The right honorable minister was asked to give the answer to 7 x 8 and he gave the answer of 54, instead of the correct 56. His error prompted widespread ridicule in the national media, accompanied by calls for a stronger emphasis on ‘times table’ memorization in schools. This past September the Conservative education minister for England, a man with no education experience, insisted that all students in England memorize all their times tables up to 12 x 12 by the age of 9. This requirement has now been placed into the UK’s mathematics curriculum and will result, I predict, in rising levels of math anxiety and students turning away from mathematics in record numbers. The US is moving in the opposite direction, as the new Common Core State Standards (CCSS) de-emphasize the rote memorization of math facts. Unfortunately misinterpretations of the meaning of the word ‘fluency’ in the CCSS are commonplace and publishers continue to emphasize rote memorization, encouraging the persistence of damaging classroom practices across the United States.
Mathematics facts are important but the memorization of math facts through times table repetition, practice and timed testing is unnecessary and damaging. The English minister’s mistake when he was asked 7 x 8 prompted calls for more memorization. This was ironic as his mistake revealed the limitations of memorization without ‘number sense’. People with number sense are those who can use numbers flexibly. When asked to solve 7 x 8 someone with number sense may have memorized 56 but they would also be able to work out that 7 x 7 is 49 and then add 7 to make 56, or they may work out ten 7’s and subtract two 7’s (70-14). They would not have to rely on a distant memory. Math facts, themselves, are a small part of mathematics and they are best learned through the use of numbers in different ways and situations. Unfortunately many classrooms focus on math facts in unproductive ways, giving students the impression that math facts are the essence of mathematics, and, even worse that the fast recall of math facts is what it means to be a strong mathematics student. Both of these ideas are wrong and it is critical that we remove them from classrooms, as they play a large role in the production of math anxious and disaffected students.
It is useful to hold some math facts in memory. I don’t stop and think about the answer to 8 plus 4, because I know that math fact. But I learned math facts through using them in different mathematical situations, not by practicing them and being tested on them. I grew up in the progressive era of England, when primary schools focused on the ‘whole child’ and I was not presented with tables of addition, subtraction or multiplication facts to memorize in school. This has never held me back at any time or place in my life, even though I am a mathematics education professor. That is because I have number sense, something that is much more important for students to learn, and that includes learning of math facts along with deep understanding of numbers and the ways they relate to each other.
Number Sense
In a critical research project researchers studied students as they solved number problems (Gray & Tall, 1994). The students, aged 7 to 13, had been nominated by their teachers as being low, middle or high achieving. The researchers found an important difference between the low and high achieving students – the high achieving students used number sense, the low achieving students did not. The high achievers approached problems such as 19 + 7 by changing the problem into, for example, 20 + 6. No students who had been nominated as low achieving used number sense. When the low achieving students were given subtraction problems such as 21-16 they counted backwards, starting at 21 and counting down, which is extremely difficult to do. The high achieving students used strategies such as changing the numbers into 20 -15 which is much easier to do. The researchers concluded that low achievers are often low achievers not because they know less but because they don’t use numbers flexibly – they have been set on the wrong path, often from an early age, of trying to memorize methods instead of interacting with numbers flexibly (Boaler, 2009). This incorrect pathway means that they are often learning a harder mathematics and sadly, they often face a lifetime of mathematics problems.
Number sense is the foundation for all higher-level mathematics (Feikes & Schwingendorf, 2008). When students fail algebra it is often because they don’t have number sense. When students work on rich mathematics problems – such as those we provide at the end of this paper – they develop number sense and they also learn and can remember math facts. When students focus on memorizing times tables they often memorize facts without number sense, which means they are very limited in what they can do and are prone to making errors –such as the one that led to nationwide ridicule for the British politician. Lack of number sense has led to more catastrophic errors, such as the Hubble Telescope missing the stars it was intended to photograph in space. The telescope was looking for stars in a certain cluster but failed due to someone making an arithmetic error in the programming of the telescope (LA Times, 1990). Number sense, critically important to students’ mathematical development, is inhibited by over-emphasis on the memorization of math facts in classrooms and homes. The more we emphasize memorization to students the less willing they become to think about numbers and their relations and to use and develop number sense (Boaler, 2009).
The Brain and Number Sense
Some students are not as good at memorizing math facts as others. That is something to be celebrated, it is part of the wonderful diversity of life and people. Imagine how dull and unispiring it would be if teachers gave tests of math facts and everyone answered them in the same way and at the same speed as though they were all robots. In a recent brain study scientists examined students’ brains as they were taught to memorize math facts. They saw that some students memorized them much more easily than others. This will be no surprise to readers and many of us would probably assume that those who memorized better were higher achieving or “more intelligent” students. But the researchers found that the students who memorized more easily were not higher achieving, they did not have what the researchers described as more “math ability”, nor did they have higher IQ scores (Supekar et al, 2013). The only differences the researchers found were in a brain region called the hippocampus, which is the area of the brain that is responsible for memorized facts (Supekar et al, 2013). Some students will be slower when memorizing but they still have exceptional mathematics potential. Math facts are a very small part of mathematics but unfortunately students who don’t memorize math facts well often come to believe that they can never be successful with math and turn away from the subject.
Teachers across the US and the UK ask students to memorize multiplication facts, and sometimes addition and subtraction facts too, usually because curriculum standards have specified that students need to be “fluent with numbers”. Parish, drawing from Fosnot and Dolk (2001) defines fluency as ‘knowing how a number can be composed and decomposed and using that information to be flexible and efficient with solving problems.’ (Parish 2014, p 159). Whether or not we believe that fluency requires more than the recall of math facts, research evidence points in one direction: The best way to develop fluency with numbers is to develop number sense and to work with numbers in different ways, not to blindly memorize without number sense.
When teachers emphasize the memorization of facts, and give tests to measure number facts students suffer in two important ways. For about one third of students the onset of timed testing is the beginning of math anxiety (Boaler, 2014). Sian Beilock and her colleagues have studied people’s brains through MRI imaging and found that math facts are held in the working memory section of the brain. But when students are stressed, such as when they are taking math questions under time pressure, the working memory becomes blocked and students cannot access math facts they know (Beilock, 2011; Ramirez, et al, 2013). As students realize they cannot perform well on timed tests they start to develop anxiety and their mathematical confidence erodes. The blocking of the working memory and associated anxiety particularly occurs among higher achieving students and girls. Conservative estimates suggest that at least a third of students experience extreme stress around timed tests, and these are not the students who are of a particular achievement group, or economic background. When we put students through this anxiety provoking experience we lose students from mathematics.
Math anxiety has now been recorded in students as young as 5 years old (Ramirez, et al, 2013) and timed tests are a major cause of this debilitating, often life-long condition. But there is a second equally important reason that timed tests should not be used – they prompt many students to turn away from mathematics. In my classes at Stanford University, I experience many math traumatized undergraduates, even though they are among the highest achieving students in the country. When I ask them what has happened to lead to their math aversion many of the students talk about timed tests in second or third grade as a major turning point for them when they decided that math was not for them. Some of the students, especially women, talk about the need to understand deeply, which is a very worthwhile goal, and being made to feel that deep understanding was not valued or offered when timed tests became a part of math class. They may have been doing other more valuable work in their mathematics classes, focusing on sense making and understanding, but timed tests evoke such strong emotions that students can come to believe that being fast with math facts is the essence of mathematics. This is extremely unfortunate. We see the outcome of the misguided school emphasis on memorization and testing in the numbers dropping out of mathematics and the math crisis we currently face (see www.youcubed.org). When my own daughter started times table memorization and testing at age 5 in England she started to come home and cry about maths. This is not the emotion we want students to associate with mathematics and as long as we keep putting students under pressure to recall facts at speed we will not erase the widespread anxiety and dislike of mathematics that pervades the US and UK (Silva & White, 2013; National Numeracy, 2014).
In recent years brain researchers have found that the students who are most successful with number problems are those who are using different brain pathways – one that is numerical and symbolic and the other that involves more intuitive and spatial reasoning (Park & Brannon, 2013). At the end of this paper we give many activities that encourage visual understanding of number facts, to enable important brain connections. Additionally brain researchers have studied students learning math facts in two ways – through strategies or memorization. They found that the two approaches (strategies or memorization) involve two distinct pathways in the brain and that both pathways are perfectly good for life long use. Importantly the study also found that those who learned through strategies achieved ‘superior performance’ over those who memorized, they solved problems at the same speed, and showed better transfer to new problems. The brain researchers concluded that automaticity should be reached through understanding of numerical relations, achieved through thinking about number strategies (Delazer et al, 2005).
Why is Mathematics Treated Differently?
In order to learn to be a good English student, to read and understand novels, or poetry, students need to have memorized the meanings of many words. But no English student would say or think that learning about English is about the fast memorization and fast recall of words. This is because we learn words by using them in many different situations – talking, reading, and writing. English teachers do not give students hundreds of words to memorize and then test them under timed conditions. All subjects require the memorization of some facts, but mathematics is the only subject in which teachers believe they should be tested under timed conditions. Why do we treat mathematics in this way?
Mathematics already has a huge image problem. Students rarely cry about other subjects, nor do they believe that other subjects are all about memorization or speed. The use of teaching and parenting practices that emphasize the memorization of math facts is a large part of the reason that students disconnect from math. Many people will argue that math is different from other subjects and it just has to be that way – that math is all about getting correct answers, not interpretation or meaning. This is another misconception. The core of mathematics is reasoning – thinking through why methods make sense and talking about reasons for the use of different methods (Boaler, 2013). Math facts are a small part of mathematics and probably the least interesting part at that. Conrad Wolfram, of Wolfram-Alpha, one of the world’s leading mathematics companies, speaks publicly about the breadth of mathematics and the need to stop seeing mathematics as calculating. Neither Wolfram nor I are arguing that schools should not teach calculating, but the balance needs to change, and students need to learn calculating through number sense, as well as spend more time on the under-developed but critical parts of mathematics such as problem solving and reasoning.
It is important when teaching students number sense and number facts never to emphasize speed. In fact this is true for all mathematics. There is a common and damaging misconception in mathematics – the idea that strong math students are fast math students. I work with a lot of mathematicians and one thing I notice about them is that they are not particularly fast with numbers, in fact some of them are rather slow. This is not a bad thing, they are slow because they think deeply and carefully about mathematics. Laurent Schwartz, a top mathematician, wrote an autobiography about his school days and how he was made to feel “stupid” because he was one of the slowest math thinkers in his class (Schwartz, 2001). It took him many years of feeling inadequate to come to the conclusion that: ‘rapidity doesn’t have a precise relation to intelligence. What is important is to deeply understand things and their relations to each other. This is where intelligence lies. The fact of being quick or slow isn’t really relevant.’ (Schwartz, 2001) Sadly speed and test driven math classrooms lead many students who are slow and deep thinkers, like Schwartz, to believe that they cannot be good at math.
Math ‘Fluency’ and the Curriculum
In the US the new Common Core curriculum includes ‘fluency’ as a goal. Fluency comes about when stu- dents develop number sense, when they are mathematically confident because they understand numbers. Unfortunately the word fluency is often misinterpreted. ‘Engage New York’ is a curriculum that is becom- ing increasingly popular in the US that has incorrectly interpreted fluency in the following ways:
Fluency: Students are expected to have speed and accuracy with simple calculations; teachers structure class time and/or homework time for students to memorize, through repetition, core functions such as multiplication tables so that they are more able to understand and manipulate more complex functions. (Engage New York)
There are many problems with this directive. Speed and memorization are two directions that we urgently need to move away from, not towards. Just as problematically ‘Engage New York’ links the memorization of number facts to students’ understanding of more complex functions, which is not supported by research evidence. What research tells us is that students understand more complex functions when they have num- ber sense and deep understanding of numerical principles, not blind memorization or fast recall (Boaler, 2009). I am currently working with PISA analysts at the OECD. The PISA team not only issues interna- tional mathematics tests every 4 years they collect data on students’ mathematical strategies. Their data from 13 million 15-year olds across the world show that the lowest achieving students are those who focus on memorization and who believe that memorizing is important when studying for mathematics (Boaler & Zoido, in press). This idea starts early in classrooms and is one we need to eradicate. The highest achievers in the world are those who focus on big ideas in mathematics, and connections between ideas. Students develop a connected view of mathematics when they work on mathematics conceptually and blind memorization is replaced by sense making.
In the UK directives have similar potential for harm. The new national curriculum states that all students should have ‘memorised their multiplication tables up to and including the 12 multiplication table’ by the age of 9 and whilst students can memorize multiplication facts to 12 x 12 through rich engaging activities this directive is leading teachers to give multiplication tables to students to memorize and then be tested on. A leading group in the UK, led by children’s author and poet Michael Rosen, has formed to highlight the damage of current policies in schools and the numbers of primary age children who now walk to school crying from the stress they are under, caused by over-testing (Garner, The Independent, 2014). Mathemat- ics is the leading cause of students’ anxiety and fear and the unnecessary focus on memorized math facts in the early years is one of the main reasons for this.
Activities to Develop Number Facts and Number Sense
Teachers should help students develop math facts, not by emphasizing facts for the sake of facts or using ‘timed tests’ but by encouraging students to use, work with and explore numbers. As students work on meaningful number activities they will commit math facts to heart at the same time as understanding numbers and math. They will enjoy and learn important mathematics rather than memorize, dread and fear mathematics.
Number Talks
One of the best methods for teaching number sense and math facts at the same time is a teaching strategy called ‘number talks’, developed by Ruth Parker and Kathy Richardson. This is an ideal short teaching activity that teachers can start lessons with or parents can do at home. It involves posing an abstract math problem such as 18 x 5 and asking students to solve the problem mentally. The teacher then collects the different methods and looks at why they work. For example a teacher may pose 18 x 5 and find that students solve the problem in these different ways:
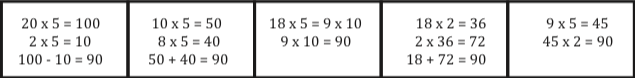
Students love to give their different strategies and are usually completely engaged and fascinated by the different methods that emerge. Students learn mental math, they have opportunities to memorize math facts and they also develop conceptual understanding of numbers and of the arithmetic properties that are critical to success in algebra and beyond. Parents can use a similar strategy by asking for their children’s methods and discussing the different methods that can be used. Two books, one by Cathy Humphreys and Ruth Parker (in press) and another by Sherry Parish (2014) illustrate many different number talks to work on with secondary and elementary students, respectively.
Research tells us that the best mathematics classrooms are those in which students learn number facts and number sense through engaging activities that focus on mathematical understanding rather than rote memorization. The following five activities have been chosen to illustrate this principle; the appendix to this document provides a greater range of activities and links to other useful resources that will help stu- dents develop number sense.
Addition Fact Activities
 Snap It: This is an activity that children can work on in groups. Each child makes a train of connecting cubes of a specified number. On the signal “Snap,” children break their trains into two parts and hold one hand behind their back. Children take turns going around the circle showing their re- maining cubes. The other children work out the full number combination. For example, if I have 8 cubes in my number train I could snap it and put 3 behind my back. I would show my group the remaining 5 cubes and they should be able to say that three are missing and that 5 and 3 make 8.
Snap It: This is an activity that children can work on in groups. Each child makes a train of connecting cubes of a specified number. On the signal “Snap,” children break their trains into two parts and hold one hand behind their back. Children take turns going around the circle showing their re- maining cubes. The other children work out the full number combination. For example, if I have 8 cubes in my number train I could snap it and put 3 behind my back. I would show my group the remaining 5 cubes and they should be able to say that three are missing and that 5 and 3 make 8.
How Many Are Hiding? In this activity each child has the same number of cubes and a cup. They take turns hiding some of their cubes in the cup and showing the leftovers. Other children work out the answer to the question “How many are hiding,” and say the full number combination.
Example: I have 10 cubes and I decide to hide 4 in my cup. My group can see that I only have 6 cubes. Stu- dents should be able to say that I’m hiding 4 cubes and that 6 and 4 make 10.
Multiplication Fact Activities
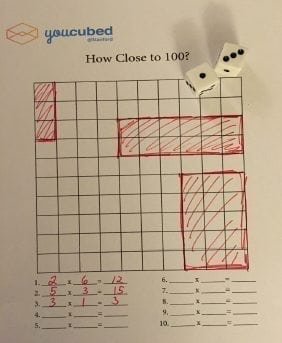 How Close to 100? This game is played in partners. Two children share a blank 100 grid. The first partner rolls two number dice. The numbers that come up are the numbers the child uses to make an array on the 100 grid. They can put the array anywhere on the grid, but the goal is to fill up the grid to get it as full as possible. After the player draws the array on the grid, she writes in the number sentence that describes the grid. The game ends when both players have rolled the dice and cannot put any more arrays on the grid. How close to 100 can you get?
How Close to 100? This game is played in partners. Two children share a blank 100 grid. The first partner rolls two number dice. The numbers that come up are the numbers the child uses to make an array on the 100 grid. They can put the array anywhere on the grid, but the goal is to fill up the grid to get it as full as possible. After the player draws the array on the grid, she writes in the number sentence that describes the grid. The game ends when both players have rolled the dice and cannot put any more arrays on the grid. How close to 100 can you get?
Pepperoni Pizza: In this game, children roll a dice twice. The first roll tells them how many pizzas to draw. The second roll tells them how many pepperonis to put on EACH pizza. Then they write the number sentence that will help them answer the question, “How many pepper- onis in all?”
For example, I roll a dice and get 4 so I draw 4 big pizzas. I roll again and I get 3 so I put three pepperonis on each pizza. Then I write 4 x 3 = 12 and that tells me that there are 12 pepperonis in all.
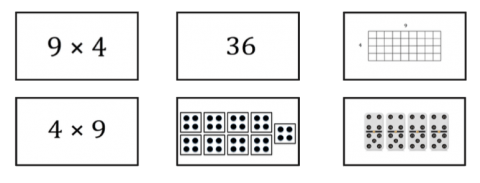
Math Cards
Many parents use ‘flash cards’ as a way of encouraging the learning of math facts. These usually include 2 unhelpful practices – memorization without understanding and time pressure. In our Math Cards activity we have used the structure of cards, which children like, but we have moved the emphasis to number sense and the understanding of multiplication. The aim of the activity is to match cards with the same numerical answer, shown through different representations. Lay all the cards down on a table and ask children to take turns picking them; pick as many as they find with the same answer (shown through any representation). For example 9 and 4 can be shown with an area model, sets of objects such as dominoes, and the number sentence. When student match the cards they should explain how they know that the different cards are equivalent. This activity encourages an understanding of multiplication as well as rehearsal of math facts. A full set of cards is given in Appendix A.
Conclusion: Knowledge is Power
The activities given above are illustrations of games and tasks in which students learn math facts at the same time as working on something they enjoy, rather than something they fear. The different activities also focus on the understanding of addition and multiplication, rather than blind memorization and this is critically important. Appendix A presents other suggested activities and references.
As educators we all share the goal of encouraging powerful mathematics learners who think carefully about mathematics as well as use numbers with fluency. But teachers and curriculum writers are often unable to access important research and this has meant that unproductive and counter-productive classroom practices continue. This short paper illustrates both the damage that is caused by the practices that often accompany the teaching of math facts – speed pressure, timed testing and blind memorization – as well as summarizes the research evidence of something very different – number sense. High achieving students use number sense and it is critical that lower achieving students, instead of working on drill and memori- zation, also learn to use numbers flexibly and conceptually. Memorization and timed testing stand in the way of number sense, giving students the impression that sense making is not important. We need to ur- gently reorient our teaching of early number and number sense in our mathematics teaching in the UK and the US. If we do not, then failure and drop out rates – already at record highs in both countries (National Numeracy, 2014; Silva & White, 2013) – will escalate. When we emphasize memorization and testing in the name of fluency we are harming children, we are risking the future of our ever-quantitative society and we are threatening the discipline of mathematics. We have the research knowledge we need to change this and to enable all children to be powerful mathematics learners. Now is the time to use it.
References
Beilock, S. (2011). Choke: What the Secrets of the Brain Reveal About Getting It Right When You Have To. New York: Free Press.
Boaler, J. (2015). What’s Math Got To Do With It? How Teachers and Parents Can Help Transform Mathematics Learning and Inspire Success. New York: Penguin.
Boaler, J. (2014). Research Suggests Timed Tests Cause Math Anxiety. Teaching Children Mathematics, 20 (8).
Boaler, J. (2013, Nov 12 2013). The Stereotypes That Distort How Americans Teach and Learn Math. The Atlantic.
Boaler, J. & Zoido, P. (in press). The Impact of Mathematics Learning Strategies upon Achievement: A Close Analysis of Pisa Data.
Delazer, M., Ischebeck, A., Domahs, F., Zamarian, L., Koppelstaetter, F., Siedentopf, C.M. Kaufmann; Benke, T., & Felber, S. (2005). Learning by Strategies and Learning by Drill – evidence from an fMRI study. NeuroImage. 839-849
Engage New York. https://schools.nyc.gov/NR/rdonlyres/9375E046-3913-4AF5-9FE3-D21BAE8FEE8D/0/CommonCoreIn- structionalShifts_Mathematics.pdf
Feikes, D. & Schwingendorf, K. (2008). The Importance of Compression in Children’s Learning of Mathematics and Teacher’s Learning to Teach Mathematics. Mediterranean Journal for Research in Mathematics Education 7 (2).
Fosnot, C, T & Dolk, M (2001). Young Mathematicians at Work: Constructing Multiplication and Division. Heinemann:
Garner, R. (October 3, 2014). The Independent. ( Link to Article )
Gray, E., & Tall, D. (1994). Duality, Ambiguity, and Flexibility: A “Proceptual” View of Simple Arithmetic. Journal for Research in Mathematics Education, 25(2), 116-140.
Humphreys, Cathy & Parker, Ruth (in press). Making Number Talks Matter: Developing Mathematical Practices and Deepen- ing Understanding, Grades 4-10. Portland, ME: Stenhouse.
LA Times (1990) https://articles.latimes.com/1990-05-10/news/mn-1461_1_math-error
Parish, S. (2014). Number Talks: Helping Children Build Mental Math and Computation Strategies, Grades K-5, Updated with Common Core Connections. Math Solutions.
Park, J. & Brannon, E. (2013). Training the Approximate Number System Improves Math Proficiency. Association for Psychological Science, 1-7
Ramirez, G., Gunderson, E., Levine, S., and Beilock, S. (2013). Math Anxiety, Working Memory and Math Achievement in Early Elementary School. Journal of Cognition and Development. 14 (2): 187–202.
Supekar, K.; Swigart, A., Tenison, C., Jolles, D., Rosenberg-Lee, M., Fuchs, L., & Menon, V. (2013). Neural Predictors of Indi- vidual Differences in Response to Math Tutoring in Primary-Grade School Children. PNAS, 110, 20 (8230-8235)
Schwartz, L. (2001). A Mathematician Grappling with His Century. Birkhäuser
Silva, E., & White, T. (2013). Pathways to Improvement: Using Psychological Strategies to help College Students Master Devel- opmental Math: Carnegie Foundation for the Advancement of Teaching.
National Numeracy (2014). https://www.nationalnumeracy.org.uk/what-the-research-says/index.html
