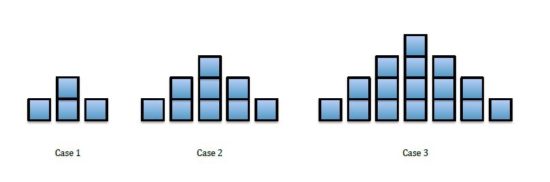
Task Instructions
We often see growth pattern tasks that focus on numerical questions like “How many squares are in the 100th case?” or “How many squares are in the nth case?” These are good questions, but we only ask them after we focus on what the shape looks like and how it grows. We start by asking students “How do you see the shapes growing?” and we ask that they make their answer entirely visual, that they forget about counting and numbers. Color coding is often a great tool for this.
Once students share how they see the growth in the pattern we then proceed to the numerical and algebraic questions. Having looked at the pattern growth visually opens up the ways of thinking about the pattern to answer the question about the 100th and the nth case. It also shows students how we all see math differently even in a question that has a single numerical answer.
As an extension of this task, we sometimes ask students to come up with algebraic expressions that match the different visual ways of seeing the pattern grow. This might give rise to a question like “Since the number of squares is the same in each way of seeing why do the algebraic representations look different?” and it might lead into a conversation about equivalent algebraic expressions and simplification. Discussions about this idea and question bridge the visual and algebraic ways of thinking and exercise the connections between different parts of the brain.
Reference
Ruth Parker and the Mathematics Education Collaborative, MEC